行业新闻
粒子群算法优化策略总结
粒子群算法优化策略总结
基于研究课题的需要,对粒子群算法的优化策略进行总结,根据所读论文,总结出对粒子群算法的优化主要在以下5个方面:
- 对于惯性权重w的优化
- 对于c1、c2的优化
- 种群优化
- 对于速度更新公式的优化
- 对于位移更新公式的优化
本篇博客会对这5个方面的优化进行总结,对于每一种具体优化,进行优化策略、参考论文、原理、作用、具体做法5个方面进行总结。
本篇博客总结的粒子群算法优化策略同样适用于其它群智能优化算法,对于优化策略的总结后面也会不断更新。
参考论文–基于混沌映射和高斯扰动的改进粒子群算法MPPT控制策略研究
注意,这里是非线性随机递增惯性权重,与非线性递减惯性权重不同。
非线性递减惯性权重,前期w取值较大,具有较强的全局搜索能力,后期w取值较小,具有较强的局部搜索能力,而非线性递增惯性权重则与之相反,前期w取值较小,具有较强的局部搜索能力,后期w取值较大,具有较强的全局搜索能力。混沌Sine映射作为一种经典的混沌映射,具有良好的遍历性等优点,增加了算法的随机性,使算法在前期拥有较强的局部寻优能力的同时,在后期也拥有不错的全局寻优能力。通过混沌sine映射产生(0,1)的随机数,使得w增长的更慢,使得其前期具有更强的局部开发能力 ,改进后的惯性权重表达式如下所示:
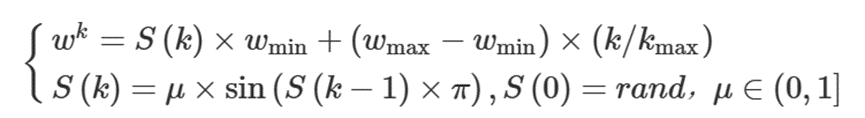
k为当前迭代次数;kmax为最大迭代次数;wk为第k次迭代时的权重值;wmax、wmin为惯性权重的上下限分别为0.9、0.4;S(k)为混沌Sine映射。
参考论文–引入Circle映射和正弦余弦因子的改进粒子群算法
惯性权重值将会随着迭代次数的不断增多而减小,并且是一种非线性、先快后慢的形式,契合了算法前期注重全局探索,后期注重局部开发的搜索特点,有利于提高算法的收敛速度和精度。
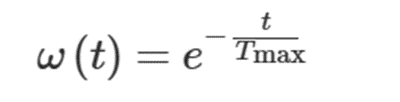
t是当前迭代次数,Tmax是设置的最大迭代次数:
该优化策略的核心思想是将种群分为三个部分,其中属于大范围搜索种群的使用策略1更改惯性权重,属于精细搜索种群的使用策略2更改惯性权重。使得不同种群的粒子在同一时期具有不同的探测能力和开发能力。

当c1较大、c2较小时,粒子群算法有着更好的全局搜索能力,当c1较小、c2较大时,有着更好的局部搜索能力。为了在初始阶段控制c1取较大值、c2取较小值,加强全局搜索能力,并且在最后迭代阶段让c1取较小值,c2取较大值加强局部搜索能力,使用正余弦函数来控制c1、c2,让c1的值能够非线性地减小,c2的值非线性地增加。
但是由于这篇论文的粒子群算法与其它粒子群算法不同,它是一种非线性递增惯性权重粒子群算法,即它在前期有着较强的局部搜索能力,后期有着较强的全局搜索能力,因此与其他粒子群算法不同,这里让c1非线性递增,c2非线性递减,使得算法在前期有着较强的局部搜索能力,在后期有着较强的全局搜索能力。具体改进公式如下所示:
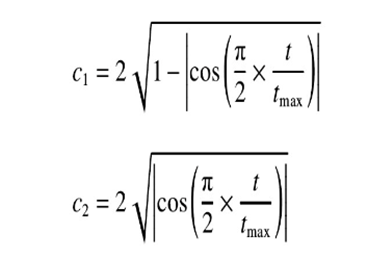
式中:wmax、wmin分别为惯性权重的最大、最小值;t和tmax分别为当前迭代次数和最大迭代次数。
参考论文–基于混沌映射和高斯扰动的改进粒子群算法MPPT控制策略研究
当c1较大、c2较小时,粒子群算法有着更好的全局搜索能力,当c1较小、c2较大时,有着更好的局部搜索能力。引入对数函数构造非线性异步学习因子来平衡算法的全局开发能力和局部搜索能力,使得在初始阶段控制c1取较大值、c2取较小值,加强全局搜索能力,并且在最后迭代阶段让c1取较小值,c2取较大值加强局部搜索能力
但是本篇论文的粒子群算法是为了让算法在前期具有较强的局部开发能力,后期要有较强的全局搜索能力,所以得让c1在前期下降的快一些,c2在前期增长的快一些,所以得让c1在前期的值较小,c2在前期的值较大。
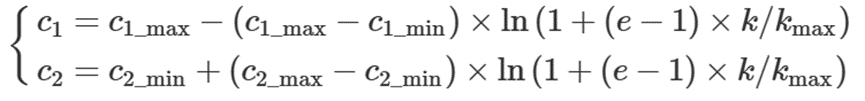
c1_max、c1_min、c2_max、c2_min为学习因子c1、c2的上下限值,分别为2.1、0.8、2.1、0.8。
参考论文–引入Circle映射和正弦余弦因子的改进粒子群算法
受SCA中的搜索机制和位置更新公式的启发,用SCA中的正弦项和余弦项来代替PSO中的学习因子。并且引入概率p。p取[0,1]之间的一个随机数,当p<0.5时,采用公式(15)更新粒子速度,否则采用公式(16)更新粒子速度。其中,ω由式(14)决定,即惯性权重优化第2种方法,r1由式(17)决定,r2是[0,2π]之间的一个随机数。
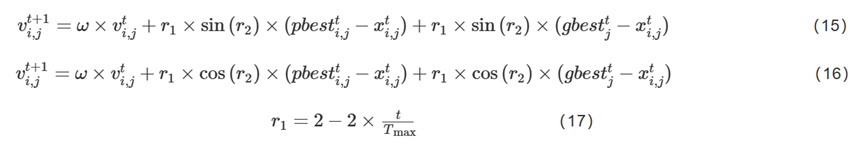
引入正弦余弦因子后,学习因子不再是简单地单调递减或单调递增的变化趋势,而是成一种在[?2,2]之间震荡式的总体衰减的趋势。结合p,概率性的切换正弦函数与余弦函数作为学习因子,使种群中各粒子围绕个体最优位置和种群最优位置进行震荡衰减性的搜索移动,不仅增加了粒子探索方向的多样性,还拓宽了粒子的探索空间。再结合指数型非线性递减的惯性权重,在算法全局探索和局部开发上实现了更好的平衡。
参考论文–引入Circle映射和正弦余弦因子的改进粒子群算法
一般使用随机初始化的操作生成初始种群,但这样得到的初始种群由于其中个体的分布并不均匀,对于算法的收敛性能有根本上的限制。基于混沌映射具有随机性、遍历性和规律性等特点,契合了初始种群的要求,经过比较和分析,本文选择采用引入Circle映射的种群初始化操作,获得更加均匀和多样的初始种群,有利于提高算法的收敛速度和精度。Circle映射产生混沌序列的表达式如下式所示,其中,numi表示第i个混沌序列数,mod(a,b)表示a对b的取余运算。
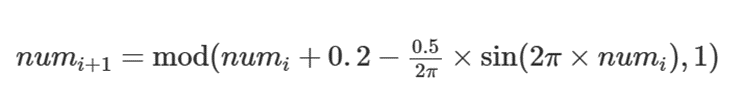
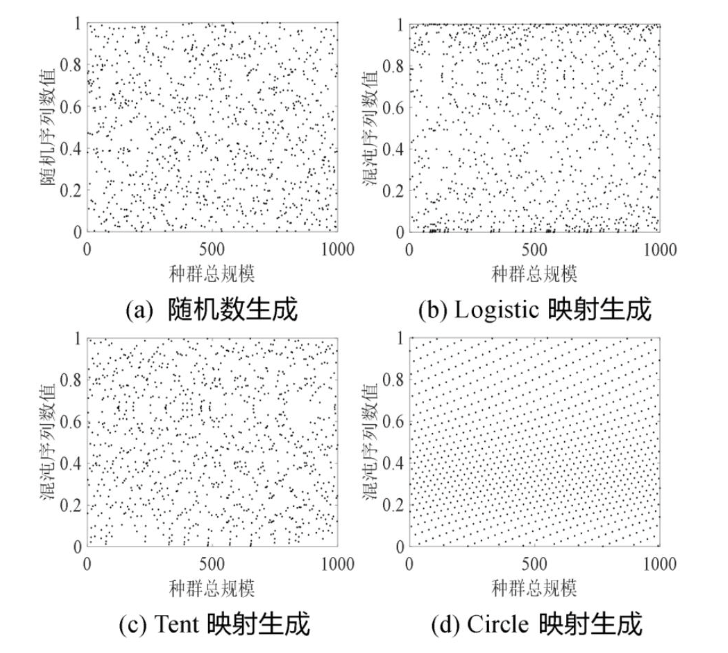
图1展示了常用随机数、Logistic映射、Tent映射和Circle映射分别产生1000个序列数值的分布图。观察图1可知,Circle映射产生的混沌序列数值在0到1之间的分布比普通随机数、Logistic映射和Tent映射产生的序列数值的分布要更加均匀,将其引入种群的初始化操作中,能为算法提供一个高质量的搜索空间,有利于提高算法的收敛精度。
本文引入Circle映射的种群初始化操作包括对速度的初始化和对位置的初始化,分别如式(12)和式(13)所示,vub和vlb分别为粒子速度的上下界,xub和xlb分别为粒子位置的上下界,numi,j和num’i,j分别是对应粒子维度上的Circle映射产生的混沌序列值。
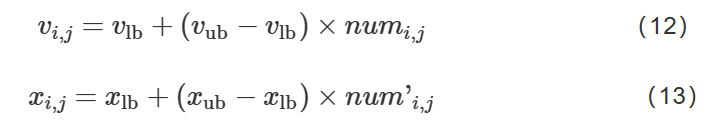
参考论文1–混合策略改进鲸鱼优化算法
参考论文2–应用档案精英学习和反向学习的多目标进化算法
参考论文3-一种精英反向学习的粒子群优化算法
因为初始种群的质量高低直接影响算法后续迭代过程的好坏与否,高质量种群可以有效地提高迭代过程中的收敛速度和精度,利用随机数随机生成初始化种群,无法保证初始化种群的质量,鉴于此,为了提高初始种群质量,避免因初始种群质量低而引发的算法收敛速度慢以及早熟现象的发生,利用精英策略和反向学习策略优化解空间。
采用精英策略选取适应度较高的个体组成新种群进行迭代,通过筛选、抛弃适应度较差的个体加速收敛和提高精度;反向策略是生成反向解,并对比、评估反向解与原解,遴选更优个体进入下次迭代,实验表明大多数精英粒子的反向解比普通粒子的反向解更靠近最优解,因此引入精英粒子的反向解可拓宽群体的活动区域,提高多样性,有利于避免算法陷入局部最优。 核心求解过程如下:
a)利用随机策略初始化鲸鱼种群W,计算、降序适应度值,筛选前n/2只鲸鱼个体组成精英种群P;
b)计算精英种群P中每个鲸鱼个体的反向解组成精英反向种群O;
c)合并初始种群W和O,依据适应度由高到低的排序规则筛选适应度值较高的前n只个体,建立新种群N。
相关定义和公式如下:

参考论文–引入Circle映射和正弦余弦因子的改进粒子群算法
首先,在算法中设置自适应随机参数A,A由式(6)决定。每次更新完粒子的位置,就对|A|的大小进行判断。当|A|>1时,就从当前的种群中随机选择20%种群规模的粒子执行带有淘汰制的随机搜索策略,即按式(9)更新每个选中的粒子的位置,并计算相应的适应度值。如果出现比目前群体最优的适应度值更低的粒子,则将该粒子位置更新为群体最优位置,然后,用这些随机搜索后的粒子位置替换目前种群中适应度值排名靠后的等量粒子位置,重组后的种群作为本次迭代后的最新种群。
本文提出一种带有淘汰制的随机搜索策略,通过条件性的随机搜索和比较更新群体最优位置的操作,可以有效地增加算法的全局探索能力;再结合淘汰制,替代种群中较差的部分个体的位置,有利于提高种群质量和增加种群中个体的多样性,增强了算法跳出局部最优的能力,更大程度上保障算法能够收敛到最优解。

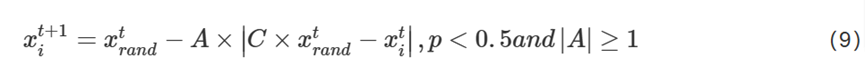
在本篇论文中,主要将粒子群分为2个种群,大范围搜索种群和精细搜索种群,不同种群的粒子采用不同的w变化策略,使得同一时期的粒子群具有不同的探测能力和开发能力。

标准PSO算法中,某粒子即使在本次寻优中寻到比上一代更优的解,按照标准 PSO 算法的速度更新公式,它依旧会在下一次寻优中更改寻优方向,这样不加区分统一对待粒子进行速度更新会降低算法的收敛速度。因此提出自适应速度更新策略,区分寻到更优解粒子和普通粒子,以提高算法的收敛速度,自适应速度更新策略公式如下:
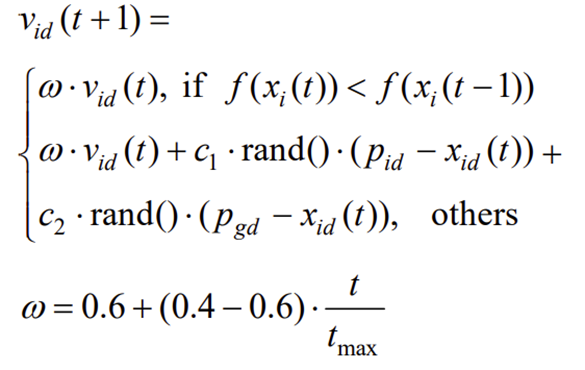
为了保证粒子在优化前期的快速性,以及保证粒子在优化后期不发散,对标准粒子群算法的公式进行调整,加入一个自适应参数来保证上述要求。
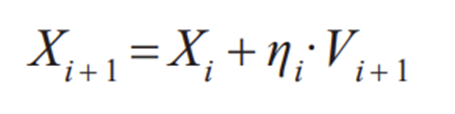

万泰新闻中心
联系我们
公司名称: 万泰-万泰平台-万泰中国加盟站
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号

