行业新闻
智能优化算法解决TSP旅行商问题--小总结
TSP问题(Traveling Saleman Problem,旅行商问题)是这样的一个问题:给定一些城市或者每对城市之间的距离,求解访问完每一座城市并回到最初出发点城市的最短回路。
它是组合优化中的NP困难问题,在运筹学和理论计算科学中有非常重要的意义。许多优化算法都是以它作为性能衡量基准。TSP问题在最坏的情况下的时间复杂度会随着城市数量的增多而成超多项式,计算量也会指数级别的增长。这个就给TSP问题的求解增加一个计算时间的约束条件。即:在最少的时间内,求解出一条遍历所有城市(并且回到最初出发点)的路线和其最短距离。
当然,TSP问题也可以分类为:(1)对称TSP问题;(2)非对称TSP问题。
(1)对称TSP问题,两个城市之间的来回距离是相等的,这样就就可以形成一个无向图。这种对称性将解的数量减少一半。也可以利用对称矩阵的方法来求解。
(2)非对称TSP问题中,即两个城市的来回距离不相等,这就形成了有向图。在交通事故、单行道和机票问题来回不对等上就是很好的非对称性问题。
本次解决的为对称TSP问题,给定的数据集分别为10个城市和200个城市的数据集,下图分别展示了城市的位置分布。
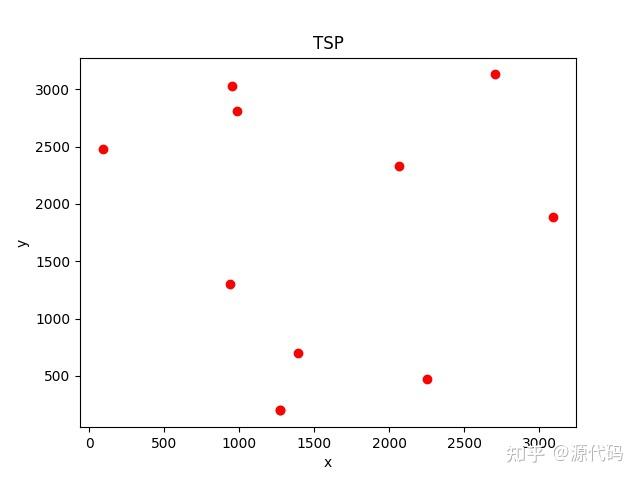
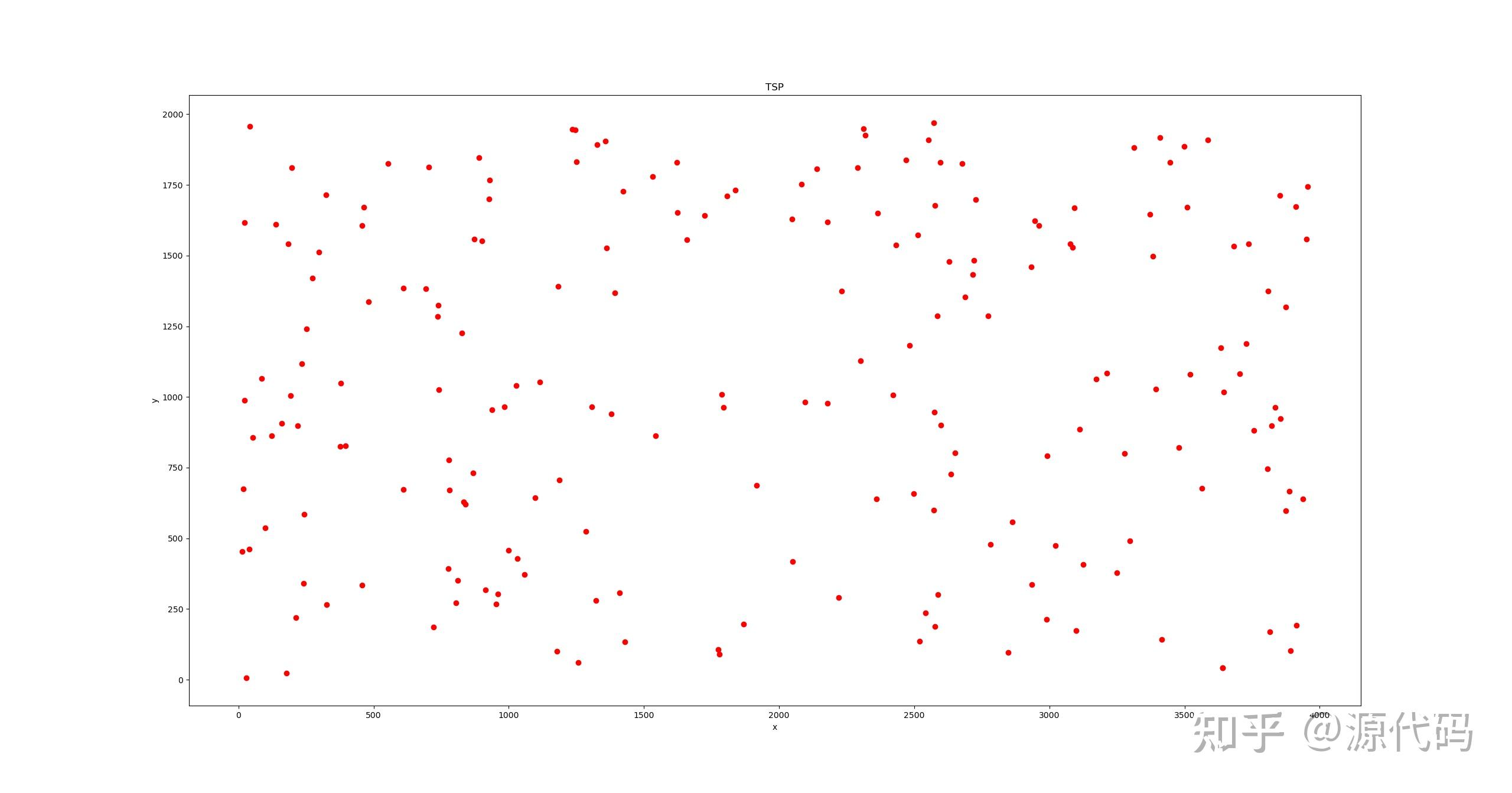
现在解决TSP问题主要有:暴力穷举法、贪心算法、分支定解算法、动态规划算法、遗传算法、蚁群算法、模拟退火算法、粒子群算法、Hopfield神经网络算法等。当然也可以利用时下比较热门的深度强化学习算法SAC来解决。
下面开始依次介绍,并且给出相关的代码(代码写的比较挫,互喷)代码主要由python和matlab编写,matlab代码主要为魔改书上的代码和网上抄来的代码(手动狗头)。

第一个就是暴力穷举法。暴力穷举法顾名思义就是直接、硬刚,列举出遍历所有点的路径,再依次计算完每个路径排列的距离之和,比较得出最短的路径即可。
求解排列的方法再python中用几行代码就可以搞定
from itertools import combinations,permutations # 导入模块
all_number = list(range(1,11))
all_p = list(permutations(all_number,len(all_number))) # 输出排列
print(len(all_p)) 统计排列数量但是问题在于:计算量随着城市数量的增长,指数级增长,非常吓人,轻轻松松爆内存。

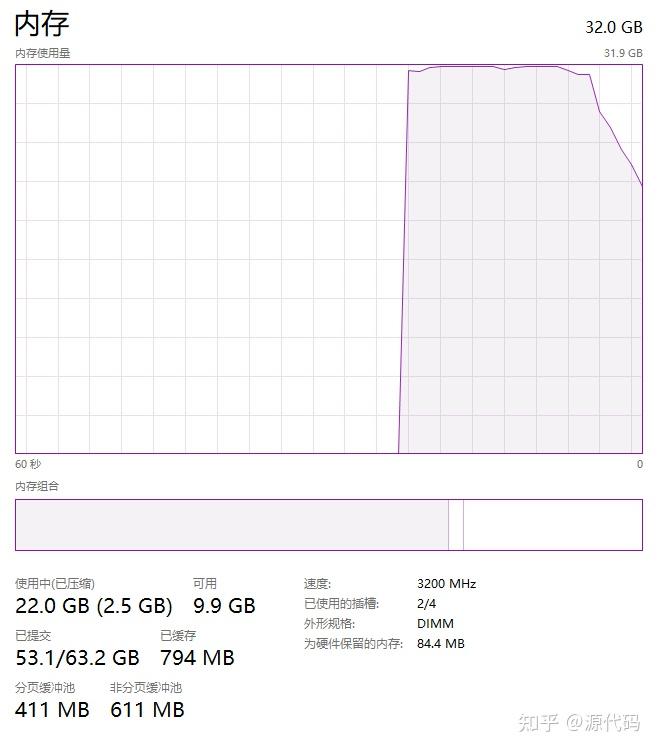
10个城市的全排列数量为:3628800。200个城市的全排列数量为:200!个。
所以这个方法一般知道就好了,在解决TSP问题中一般不会用到这个方法,但是这个方法是通用性最好,理解难度也最低的方法。
第二个算法是贪心算法。贪心算法(贪婪算法)就是在对问题进行求解时,总是做出当前看起来最优的选择,就是不从整体上进行考虑,只是得到局部意义上的最优解。
贪心不是对问题都能得到全局最优解,关键在于贪心策略的选择
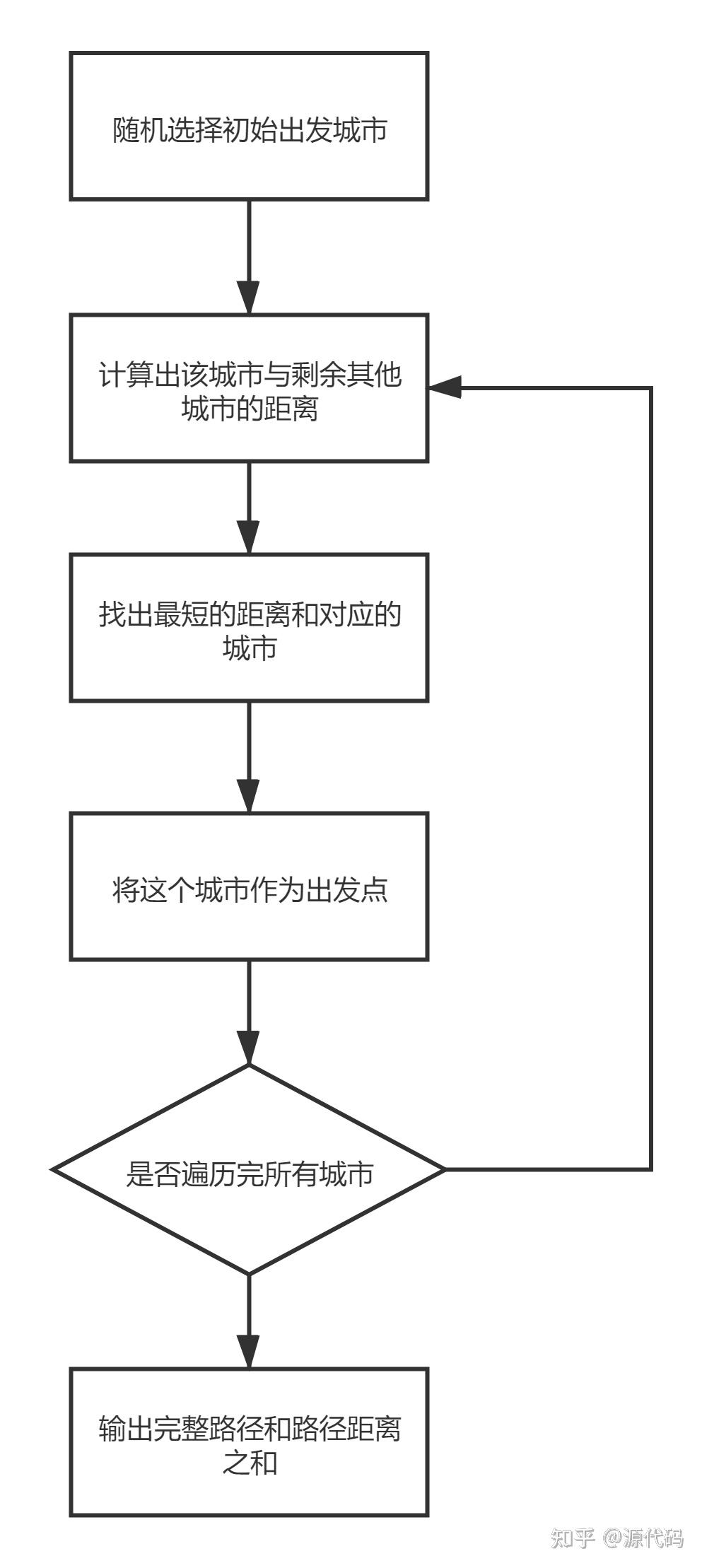
代码如下所示:
# 10个城市的地址数据
cities = [
(2066,2333),
(935,1304),
(1270,200),
(1389,700),
(984,2810),
(2253,478),
(949,3025),
(87,2483),
(3094,1883),
(2706,3130),
]
'''================找出最小距离的函数======================'''
def find_the_path(point,list):
path = []
for i in range(len(list)):
D = eucliDist(point,list[i])
path.append(D)
return path
'''================计算欧式距离==========================='''
def eucliDist(A,B):
return math.sqrt((A[0] - B[0])**2 + (A[1]-B[1])**2)
'''=================输出路线============================='''
def draw_path(x_path,y_path):
plo.plot(x_path,y_path,color = 'red') # 这里还需要把点凸显出来就可以了
plo.xlabel('x')
plo.ylabel('y')
plo.title('TSP')
plo.show() # 实现图片
'''=================找出最短的距离========================'''
frist_i = random.randint(0,199) # 任意取一个点
print(frist_i)
frist_point = cities[frist_i] # 找出这个位置上的坐标值
del cities[frist_i] # 将这个坐标从原来的列表中删除
generation = 0 # 迭代数统计
x_output = [] # 最终输出x的坐标列表,每计算出来一个点的坐标,其对应的x坐标都添加到这个列表中
y_output = [] # 最终输出y的坐标列表,同上
x_output.append(frist_point[0]) # 将出发点的x坐标添加进去
y_output.append(frist_point[1]) # 将出发点的y坐标添加进去
k = len(cities) # 城市的数量
sum_path = 0 # 最终的最短距离之和
'''
贪心算法的核心部分:每一步都是当时的最优解,全局来看可能是局部的最优解。
'''
while(generation < k):
path = find_the_path(frist_point, cities) # 计算距离初始出发点的所有距离
best_point_way = min(path) # 从所有的距离中,找出最小距离
sum_path += best_point_way # 每一次迭代计算中,最小的距离相加
points = cities[path.index(best_point_way)] # 距离出发点的距离最短的那个点
x_output.append(points[0]) # 将本次计算出的点坐标添加到最终的路线中
y_output.append(points[1]) # 同上
frist_point = points # 将points的值转移到frist_point上,为下一次迭代计算做准备
del cities[path.index(best_point_way)] # 将这个点从原来的列表中删除,这样cities中的值就会越来越少
generation += 1 # 最后迭代数增加一次
x_output.append(x_output[0]) # 在循环结束之后,将出发点坐标添加到最后,形成闭环回路
y_output.append(y_output[0]) # 同上
print(x_output)
print(y_output)
frist_point = (x_output[0],y_output[0])
final_path = eucliDist(points,frist_point) # 计算最后一个点到初始出发点的距离
sum_path += final_path # 最后的总距离一定要加上最后这段距离,才能形成闭环
print(sum_path) # 输出最终的,最短距离之和
draw_path(x_output,y_output) # 画出所有的TSP轨迹路线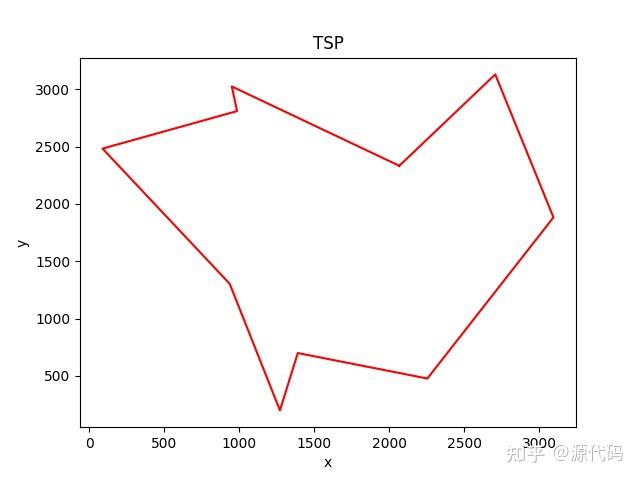
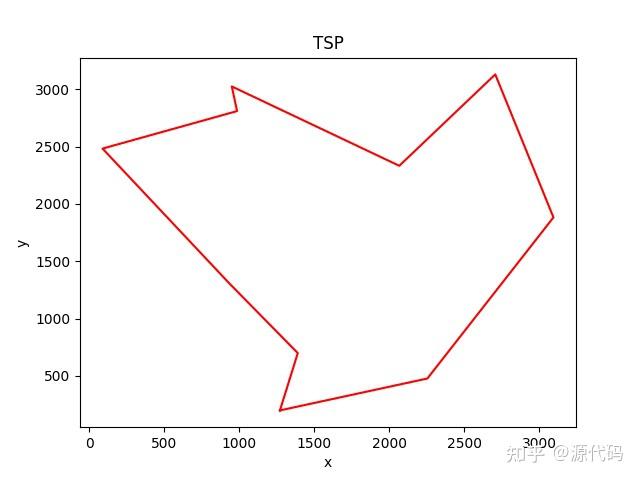
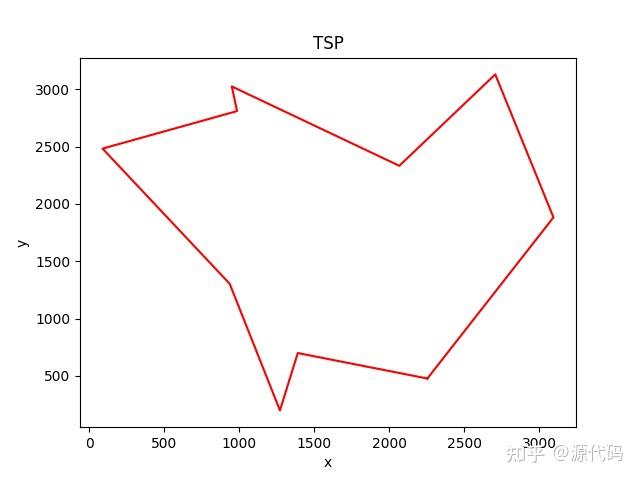
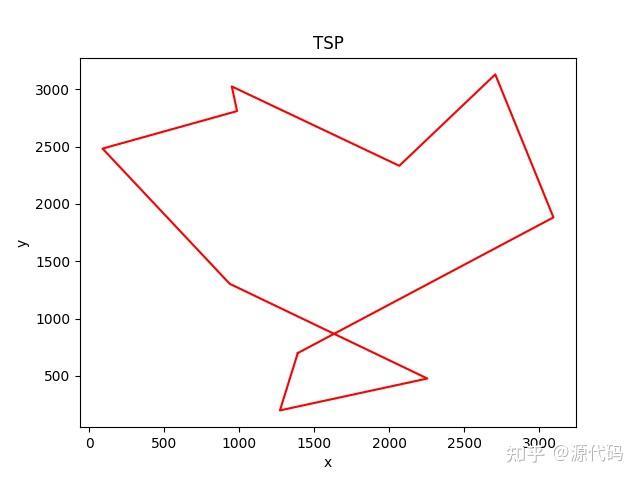
以上就是10个城市的运行结果,200个城市的运行结果比较诡异。
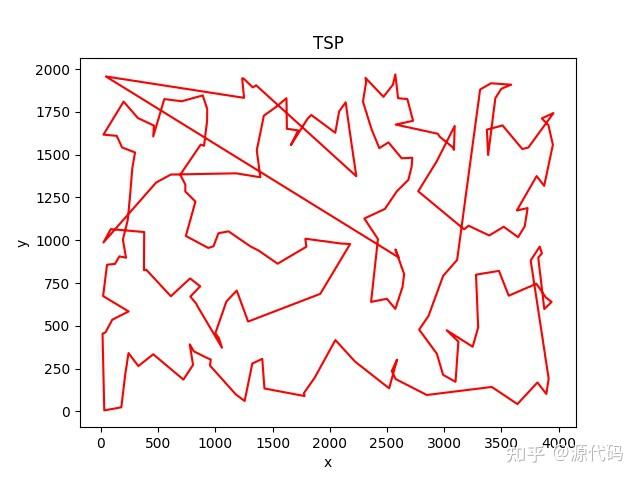
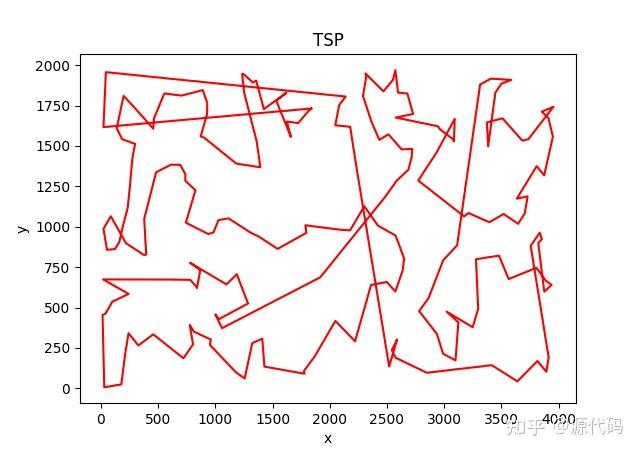
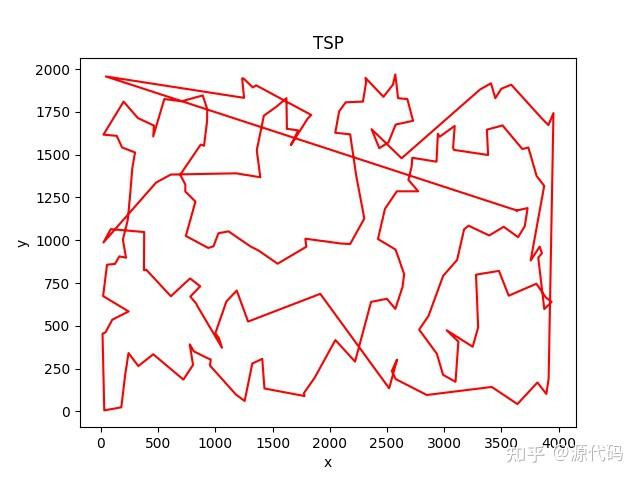
因为初始出发点的随机选择,会导致每次运行结果的不一致,也会得出不同的运算结果。
最终的运行完20次之后,10个城市比较得出了
最优解:
2—>8—>7—>5—>1—>10—>9—>6—>3—>4—>2
总距离:10127.4554
200个城市没有得出最优解。GG
第三个是分枝定界算法。分枝定界算法(branch and bound)是一种求解整数规划问题的最常用的算法,它利用广度优先搜索策略搜索和迭代的方法,选择不同的分支变量和子问题进行分支。
也可以这么理解:把全部可行解空间反复地分割为越来越小的子集,称为分支;设定一个或者多个约束条件,成为定界。每次分枝之后,约束条件之外的子集就进行剪枝操作,这样可以减少相应的计算量。
当然,这里可以把分枝定界算法和贪心策略相结合,在常规广度分枝之和,约束条件利用贪心策略。寻找每一步的最短距离,并将其作为下一步的最优解,其他进行剪枝操作。这样就可以直接得出最优解,从而省去了上面贪心算法的运行多次,比较得出最优解的问题。
'''================找出最小距离的函数======================'''
def find_the_path(point,list):
path = []
for i in range(len(list)):
D = eucliDist(point,list[i])
path.append(D)
return path
'''================计算欧式距离==========================='''
def eucliDist(A,B):
return math.sqrt((A[0] -B[0])**2 + (A[1]-B[1])**2)
'''=================输出路线============================='''
def draw_path(x_path,y_path):
plo.plot(x_path,y_path,color = 'red') # 这里还需要把点凸显出来就可以了
plo.xlabel('x')
plo.ylabel('y')
plo.title('TSP')
plo.show() # 现实图片
'''=================找出最短的距离========================'''
Optimization_solution = [] # 定义一个优化解的集合
num_cities = len(cities) # 计算城市数据集的大小 ,就是统计城市的数量
for i in range(0,num_cities): # 遍历完从0到n的数
this_turn = cities # 将列表cities的值全都复制给this_turn,这样后面的操作都不会影响cities
frist_point = this_turn[i] # 意义:将每一个点都作为初始出发点
del this_turn[i] # 将这个坐标从原来的列表中删除
generation = 0 # 迭代数统计
x_output = [] # 最终输出x的坐标列表,每计算出来一个点的坐标,其对应的x坐标都添加到这个列表中
y_output = [] # 最终输出y的坐标列表,同上
x_output.append(frist_point[0]) # 将出发点的x坐标添加进去
y_output.append(frist_point[1]) # 将出发点的y坐标添加进去
k = len(this_turn) # 城市的数量
sum_path = 0 # 最终的最短距离之和
'''
贪心算法的核心部分:每一步都是当时的最优解,全局来看可能是局部的最优解。
'''
while(generation < k):
path = find_the_path(frist_point, this_turn) # 计算距离初始出发点的所有距离
best_point_way = min(path) # 从所有的距离中,找出最小距离
sum_path += best_point_way # 每一次迭代计算中,最小的距离相加
points = this_turn[path.index(best_point_way)] # 距离出发点的距离最短的那个点
x_output.append(points[0]) # 将本次计算出的点坐标添加到最终的路线中
y_output.append(points[1]) # 同上
frist_point = points # 将points的值转移到frist_point上,为下一次迭代计算做准备
del this_turn[path.index(best_point_way)] # 将这个点从原来的列表中删除,这样cities中的值就会越来越少
generation += 1 # 最后迭代数增加一次
x_output.append(x_output[0]) # 在循环结束之后,将出发点坐标添加到最后,形成闭环回路
y_output.append(y_output[0]) # 同上
frist_point = (x_output[0],y_output[0]) # 把初始出发点找出来
final_path = eucliDist(points,frist_point) # 计算最后一个点到初始出发点的距离
sum_path += final_path # 最后的总距离一定要加上最后这段距离,才能形成闭环
# print(sum_path) # 输出最终的,最短距离之和
Optimization_solution.append(sum_path)
The_optimal_solution = min(Optimization_solution) # 找出最短距离之和
print(The_optimal_solution) # 输出最短距离第四个就是遗传算法。遗传算法(Genetic Algorithm)是一种启发式算法,模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。这种算法利用数学的方法,讲问题的求解过程转换成类似生物进化中的染色体基因交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够很快地获得较好的优化结果
其核心操作为:选择、复制、交叉、变异。
遗传算法流程:
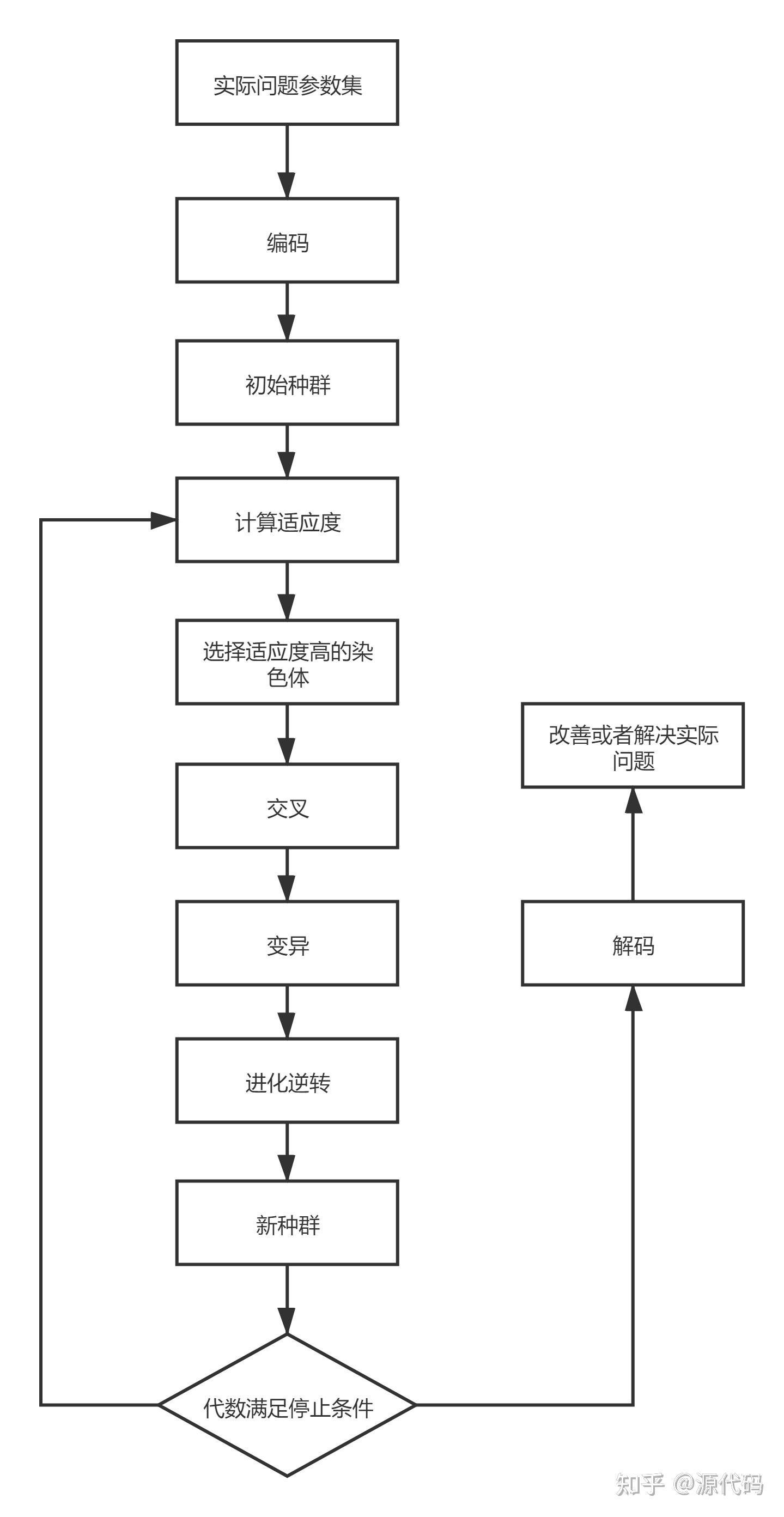
10个城市的计算结果:
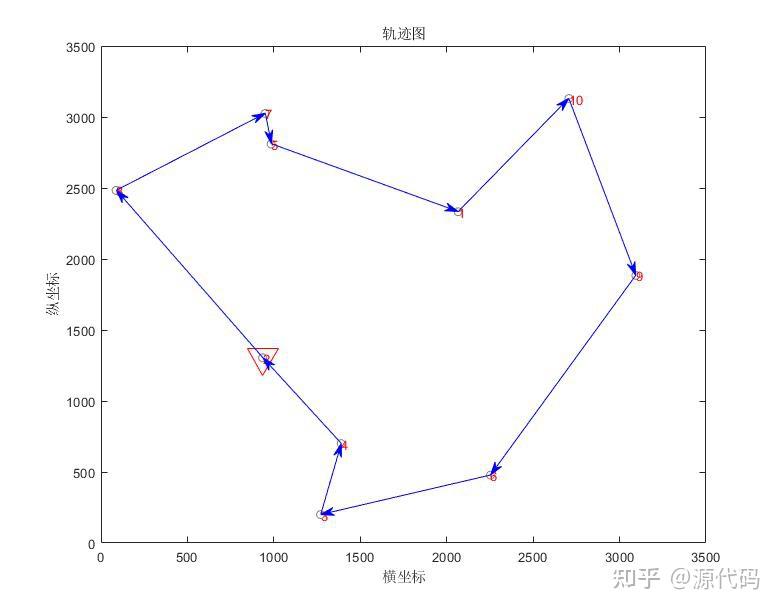
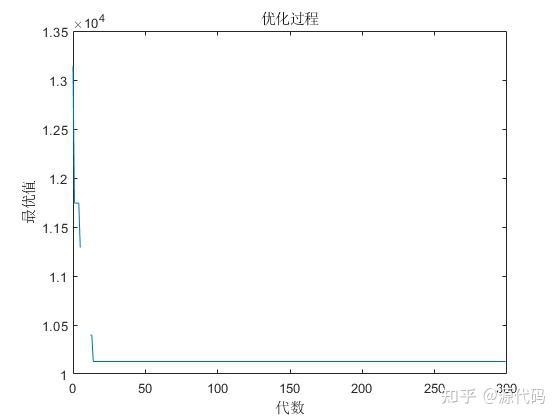
200个城市的运算结果:
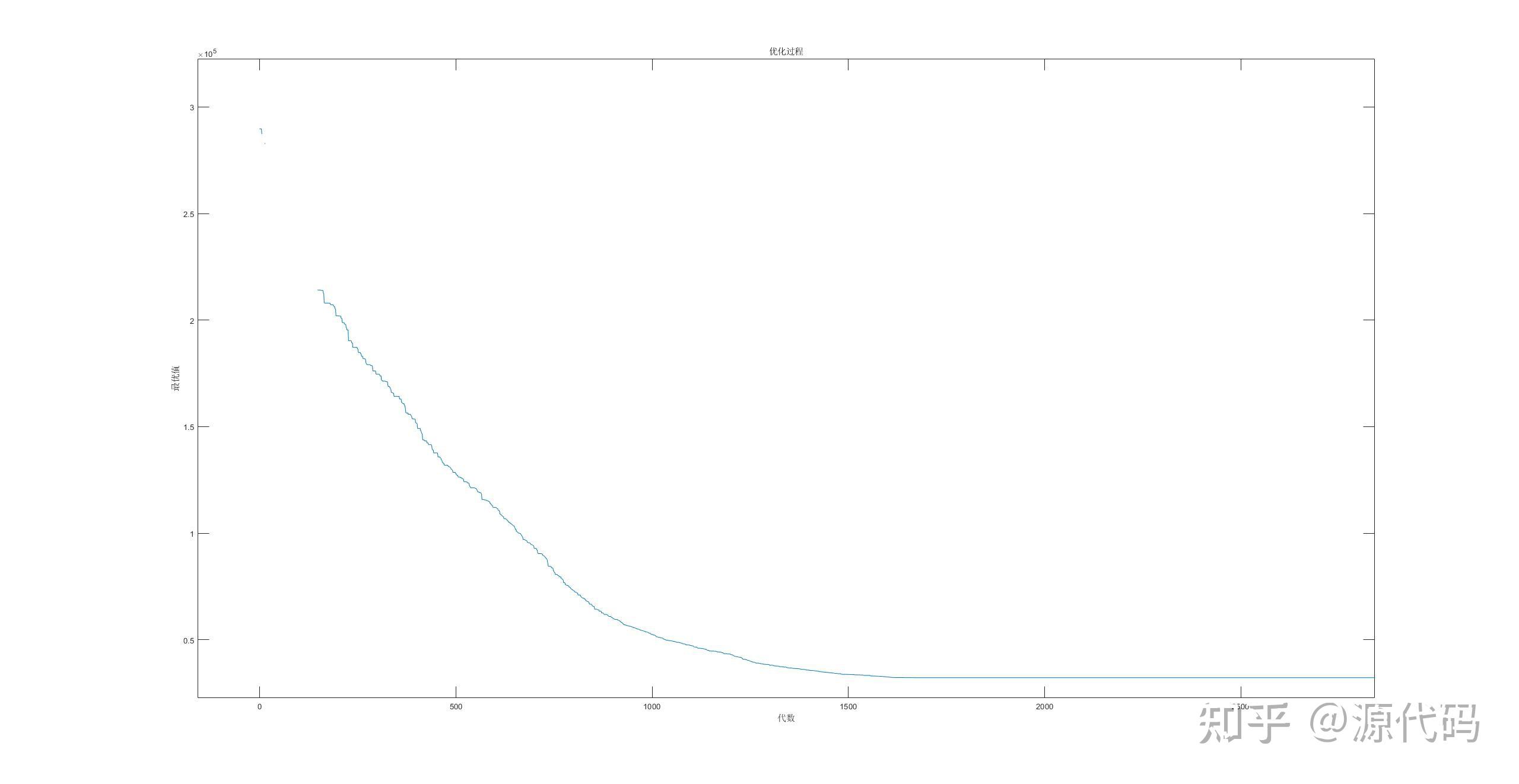
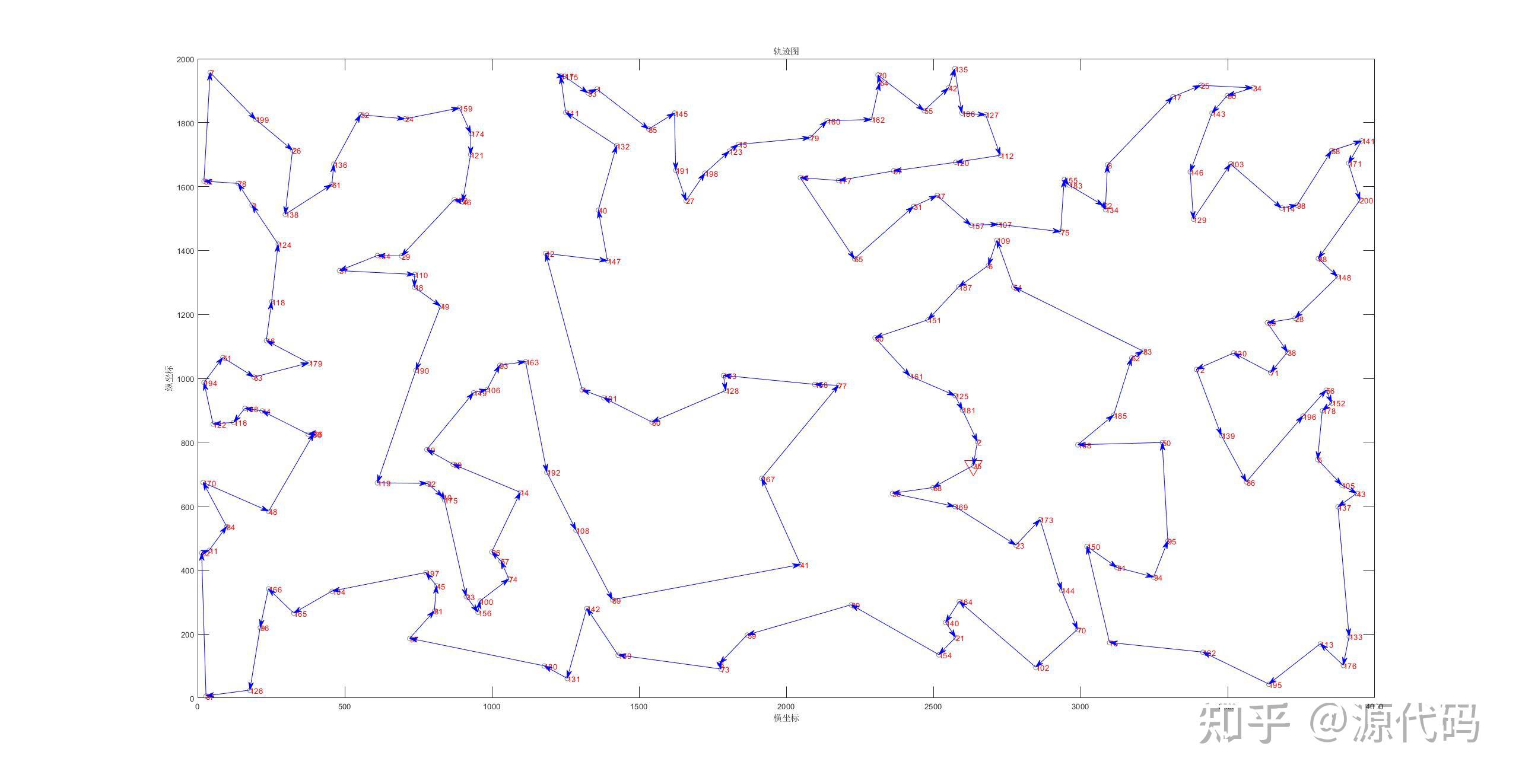
第五个就是蚁群算法。蚁群算法应用于解决优化问题的基本思路为:用蚂蚁的行走路径表示待优化问题的一种可行解,整个蚂蚁群体的所有路径就是待求解问题的所有解空间。路径较短的蚂蚁释放的信息素就会越高。随着计算的推进,较短路径上就会累计更多的信息素,这样选择该路径的蚂蚁数量也会更高。最终整个蚁群就会在正反馈的作用下集中到最佳路径上,此时就是对应待求解问题的最优解。
蚁群算法的核心:
(1)蚂蚁在携带等量的信息素一路释放
(2)信息素浓度会和路径的长度成反比
(3)下次蚂蚁来到该路口会选择信息素浓度较高的那条
(4)短的路径上的信息素浓度会越来越大,最终成为蚁群的最优路径
信息素更新的模型:
(1)蚁周模型(Ant-Cycle模型)
(2)蚁量模型(Ant-Quantity模型)
(3)蚁密模型(Ant-Density模型)
这里选择蚁周模型来作为信息更新模型。
蚁群算法流程:
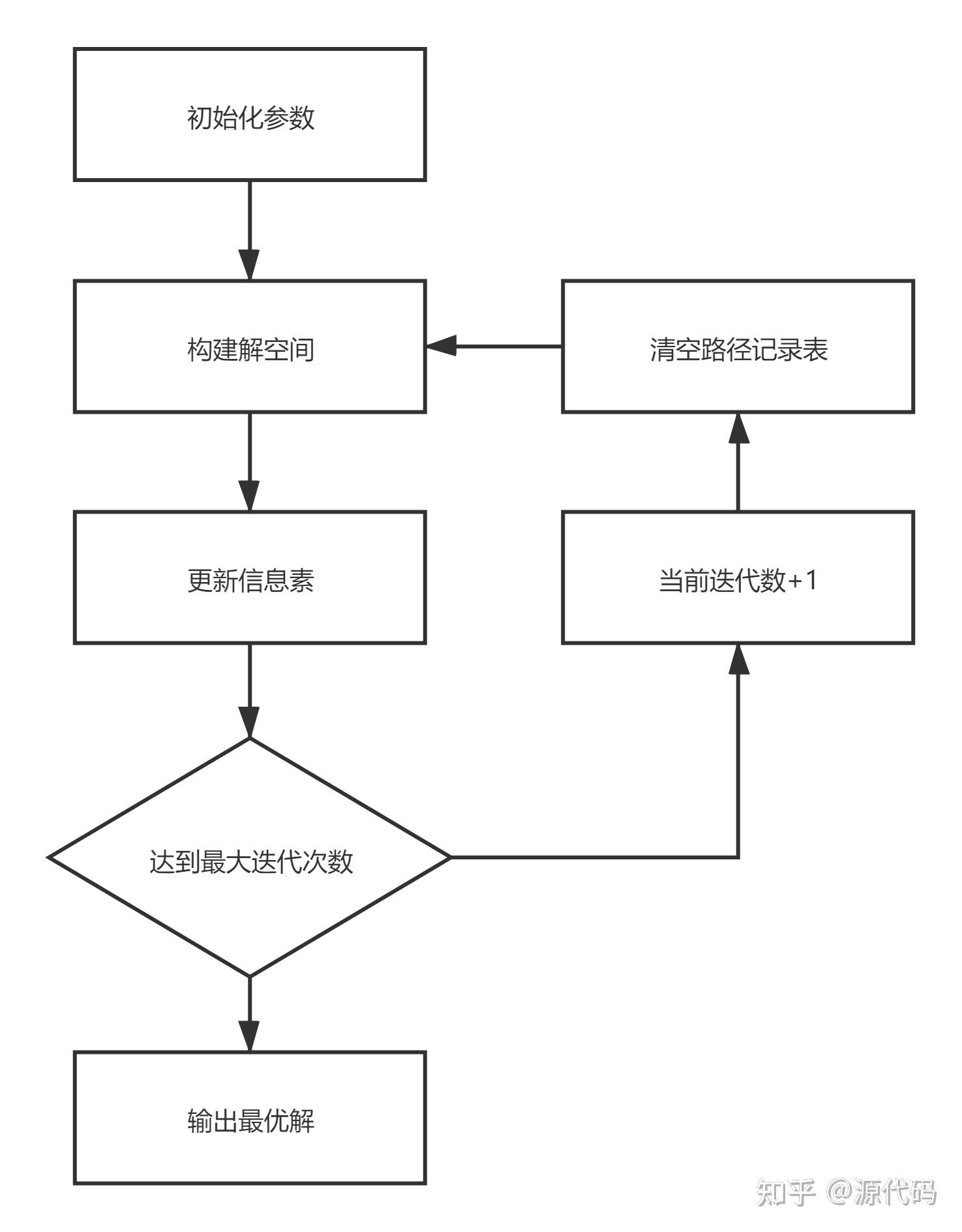
蚁群算法计算10个城市:
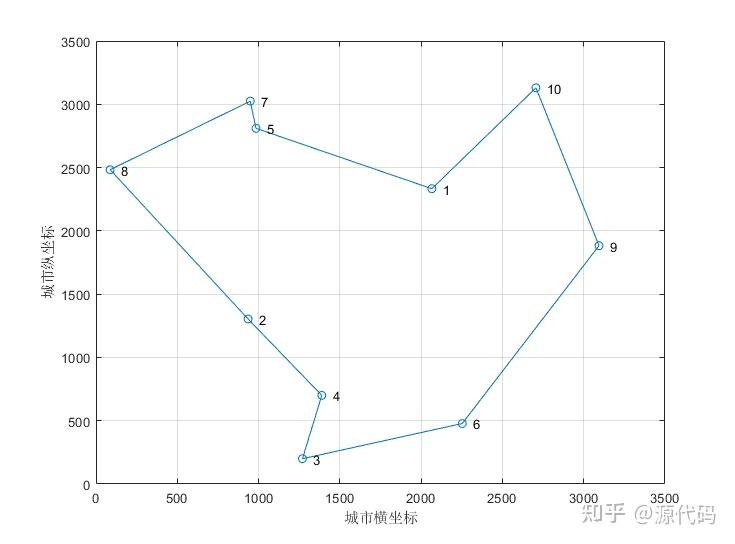
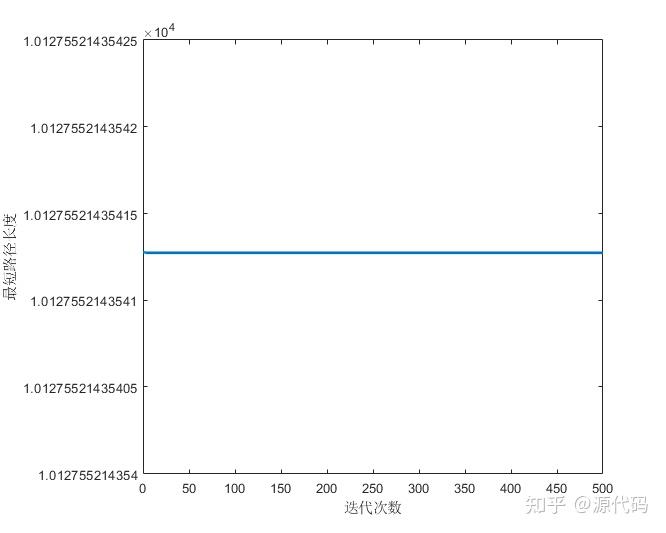
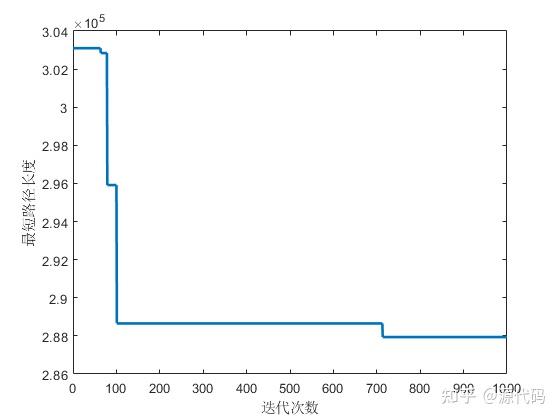
最后,这篇文章也是做的很用心:七七八八讲算法,也推荐去看看。多思考思考,可能刚开始无法理解,想的时间长了,就会理解的。
如果上面看不懂的话,也可以看看我上传的几个视频,里面会有更加详细的数学推导过程的讲解。
下面视频对应的matlab代码链接为:
链接:https://pan.baidu.com/s/1PGbDNdF3U05kvo08x3k-uA
提取码:7o4c
欢迎私信来和我讨论哦!一起变得更强!!!
万泰新闻中心
联系我们
公司名称: 万泰-万泰平台-万泰中国加盟站
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号

