什么是卡方检验，应用的条件是什么？

卡方检验就是检验两个变量之间有没有关系。

如果有兴趣可以阅读一篇我的文章，比较简单易懂

卡方检验就是检验两个变量之间有没有关系。
以运营为例:

• 卡方检验可以检验男性或者女性对线上买生鲜食品有没有区别；
• 不同城市级别的消费者对买SUV车有没有什么区别；

如果有显著区别的话，我们会考虑把这些变量放到模型或者分析里去。

那我们先从一个最简单的例子说起。
1） 根据投硬币观察到的正面，反面次数，判断这个硬币是均衡的还是不均衡。
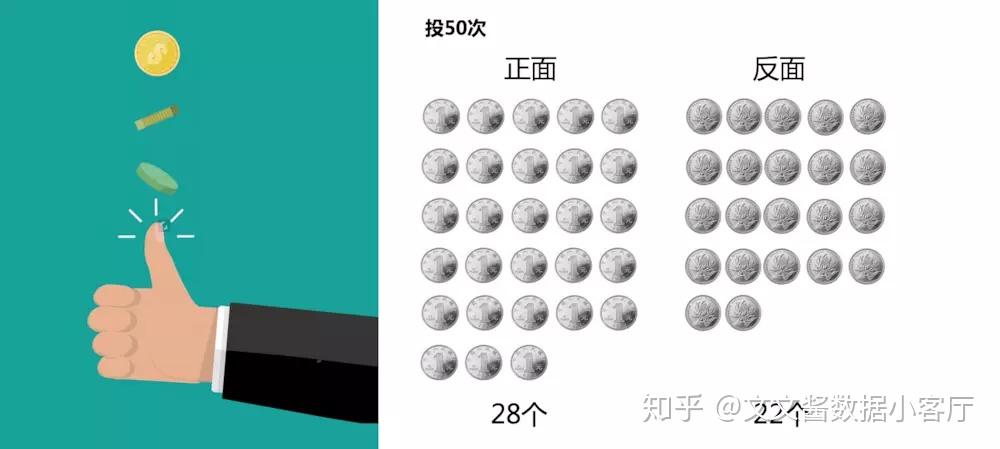
现在有一个正常的硬币，我给你投50次，你觉得会出现几个正面，几个反面？

按照你的经验你会这么思考，最好的情况肯定是25个正面，25个反面，
但是肯定不可能这么正正好好的，嗯，差不多28个正面，22个反面吧；
23个正面，27个反面也可能的，
但是10个正面，40个反面肯定不可能的，除非我运气真的那么碰巧。

你上面的这个思维方式，就是拿已经知道的结果(硬币是均衡的，没有人做过手脚)，推测出会出现的不同现象的次数。

而卡方检验是拿观察到的现象(投正面或反面的次数或者频数)，来判断这个结果(硬币是不是均衡的)。

继续上面这个例子，
如果我不知道这个硬币是不是均衡的，我想用正面，反面的频次来判断，我投了50次，
其中28个正面，22个反面。我怎么用卡方检验来证明这个硬币是均衡的还是不均衡的呢？

这里要引出卡方检验的公式：

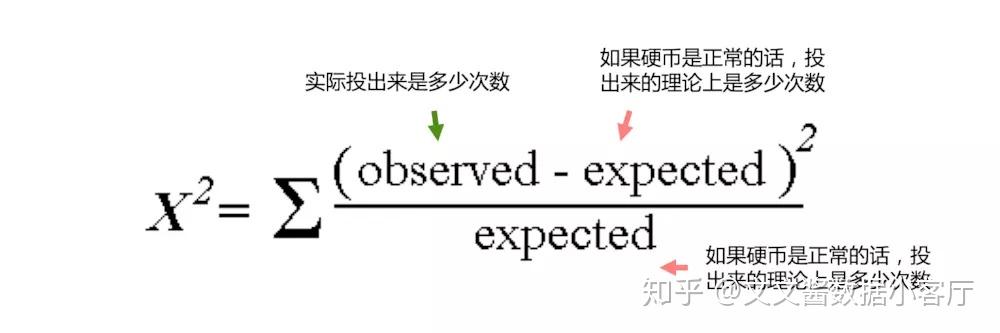
这个公式可以帮我们求出卡方检验的值，我们用

• 1 这个公式求得的值
• 2 自由度(degree of freedom，不熟悉的可以去看我在简书的用可视化思维解读统计自由度)
• 3 置信度

其中，自由度我们可以求出来，置信度的话，我们按照我们自己意愿挑选，一般我们会挑90％或者95%。

这三个数值计算方法如下：

我们拿到这3个信息，去查表，因为0.72小于查表得到的3.841，所以我们得出这个硬币是均衡的结论。

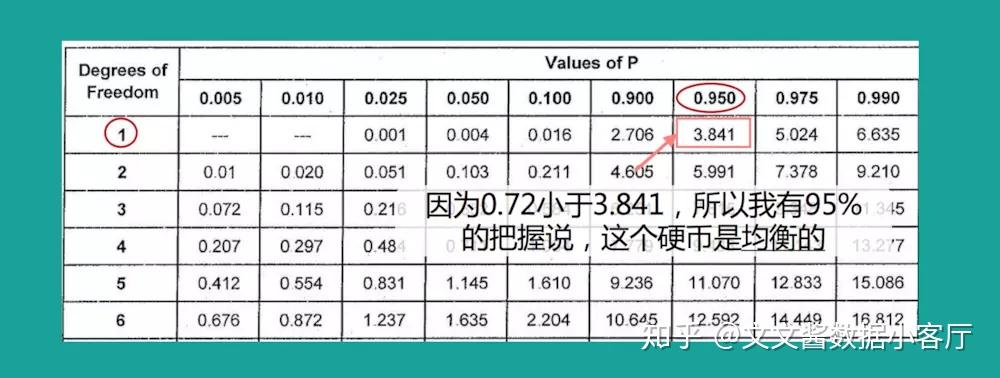
这里还涉及到假设检验中，拒绝H0还是不拒接H0，这篇文章就不详细展开了。

如果你们查表后，还是不知道是该大于的时候说均衡，还是小于的时候说均衡，那么你们可以想一下具体这个例子，
如果硬币是均衡的话，你觉得卡方的值是越小越可能是均衡的，还是越大越可能是均衡的呢？

接下来，我们再来看一个稍微难一点的例子，投骰子。
有一个筛子，我不知道它是不是均衡的，于是我打算投36次看一下。

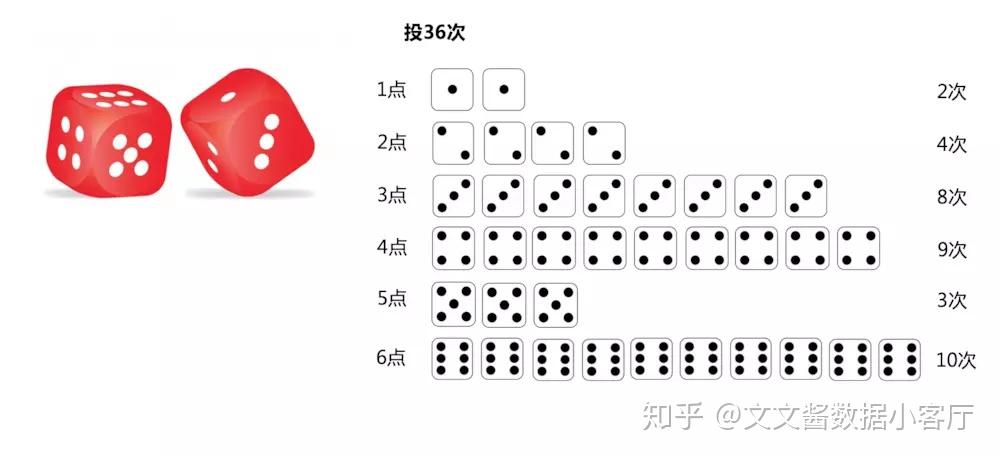
按照投硬币的方式，我先要画出一个表格，然后计算出3个数值，

带着这3个值，我们去查表，于是我们得出这个现象不能判定他是个均衡的筛子。

现在你明白其实卡方检验一点都不深奥吧。

以后如果分析师说，这个变量不显著，我把这个变量去掉了，
你就可以反问他，那卡方值是多少？
你选了多大的置信度？

最后讲个平时运营分析中的案例：

我们要观察性别和在线上买不买生鲜食品有没有关系，现实生活中，女性通常去菜市场买菜的比较多，那么在线上是不是也这样。

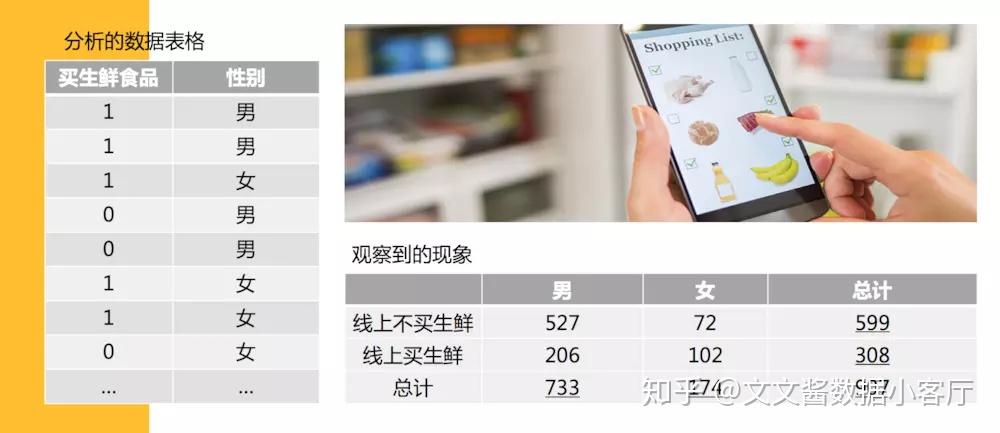
我们得出观察到数据，并且形成表格后，我们需要计算理论的数据，在上面的例子我们发现，我们发现有66%的人不在线上买生鲜（599除以907），34%的人会在线上买。 那如果，男的有733个人，女的有174个人，根据这些比例，我们可以得出的理论值是什么呢？

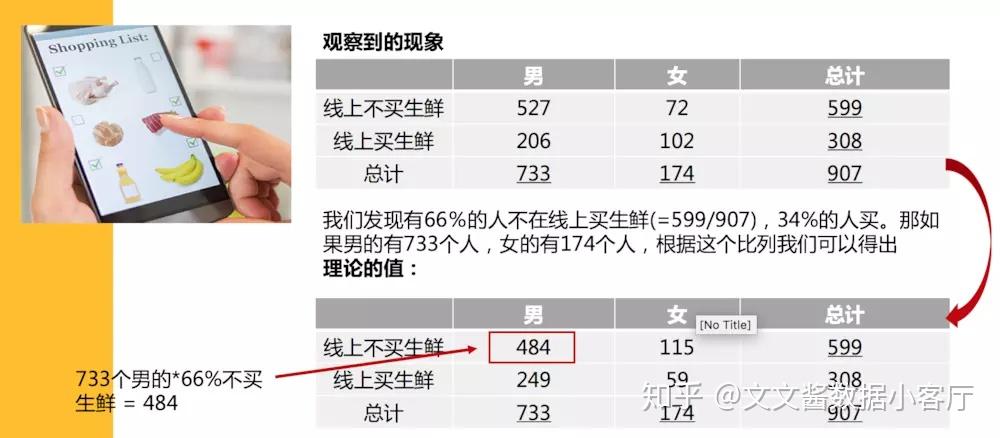
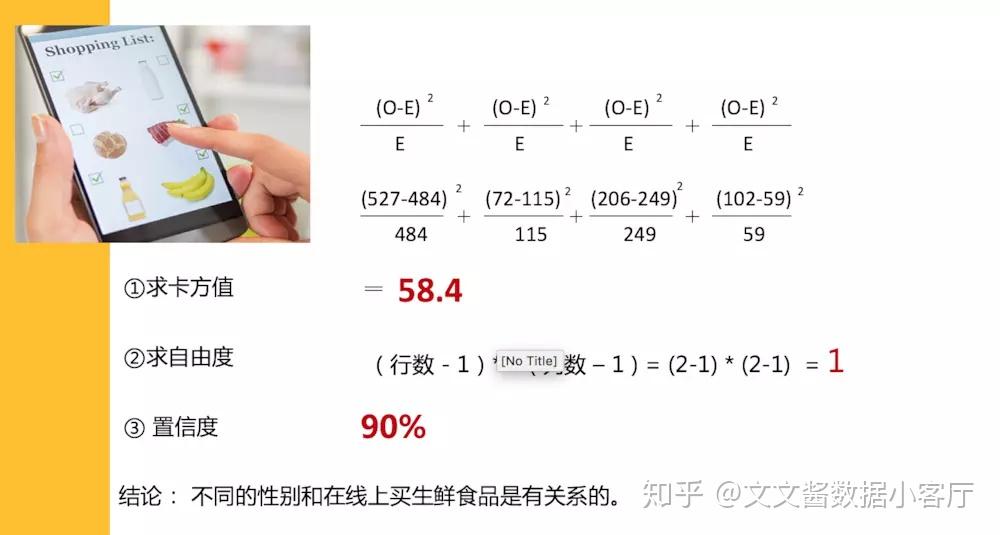
根据理论和实际值，我们可以算出卡方值，自由度，并且结合我们定义的置信度，查表得到性别和线上买生鲜是显著相关的。
所以我们如果下次看到一个女性来访问我们的网站，多投放一些广告，说不定会转化哦。

看了这几个例子，是不是觉得卡方检验一点都不复杂，其实和我们生活这么贴近，我们平时的思维方式，其实就隐含着卡方检验的道理。

如果我的文章能带给你一点点启发，还请动动你的手指，点赞、收藏、关注吧！
你的点赞和关注，是我一直写下去的动力！

卡方检验主要用于研究定类与定类数据之间的差异关系。一般使用卡方检验进行分析的目的是比较差异性。

如现状调查类问卷，以及一般调查问卷中，常使用卡方检验对样本背景信息题（性别、年龄等指标）与核心题项进行交叉分析，来说明样本背景这类指标对核心变量是否存在影响。

卡方检验要求X、Y项均为定类数据，即数字大小代表分类。

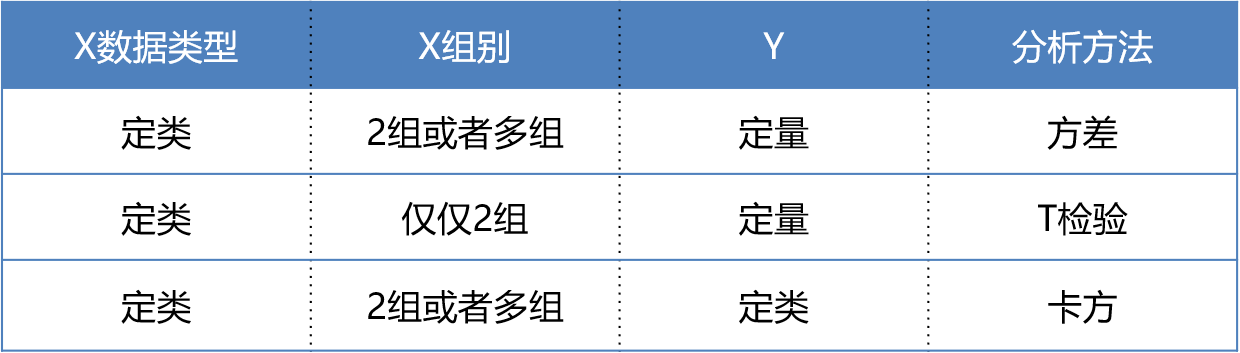
• 如果X是定类数据，Y是定量数据，且X组别多于2组，则应该使用方差分析。
• 如果X是定类数据，Y是定量数据，且X组别仅为两组，则应该使用T检验。

了解什么是卡方检验，具体对数据进行卡方检验的时候，需要借助统计软件，这里推荐使用SPSSAU，在线对各种数据进行编辑和统计分析。无需下载软件安装包，无需经过繁琐的安装过程，也不必花大量时间学习如何操作软件。

使用SPSSAU，特点是操作简单，只需两步操作即可得出分析检验结果，生成智能分析建议，而且自动提供智能化文字分析和解读，适合统计初学者。

SPSSAU还可以一步自动绘制各种图形，包括条形图、折线图、面积图、饼图、箱图、散点图、直方图等。图形的基本属性也可以很方便的自动定义，使数据分析报告更加美观。

以下以SPSSAU为分析工具，来对下列案例数据进行卡方分析：

• 案例（交叉卡方）：需要分析不同性别的人群，使用理财产品的情况是否有差别。

• 操作步骤：

第一步：只需将“性别”变量拖拽进入X变量区域，将“是否使用过理财产品”拖拽到相应Y变量区域。

第二步：点击开始卡方分析，一键得出分析结果。

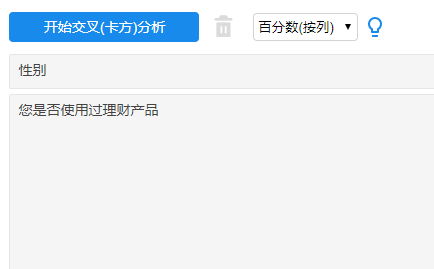
注意，这里Y项也可以根据自己实际研究需要放入多个标题，进行分析。

• 分析结果

如上图，结果已经生成了，接下来我们需要对结果进行分析解读，如何对结果进行分析，系统自动给出了分析建议，可以根据下列建议自行分析数据。如下图：

一般建议首先看P值情况，P值小于0.05或0.01即说明X与Y之间呈现出显著性，然后可以再进一步比较括号中的百分比，对每一项进行描述。

如果P>0.05了，则代表没有统计学意义，一般就不再进行深入分析。

• 智能分析：

SPSSAU不仅对检验结果提供分析建议，而且生成智能分析，自动帮你解读数据。

再如下面例子，这个案例数据格式为加权数据，我们使用卡方检验：

案例（卡方检验）：研究A、B两种药治疗感冒，两种药的疗效是否有差别？

操作步骤：放置变量位置和交叉卡方一样，只是多加了一个加权项，由自己设置，完成后点击【开始卡方检验分析】一键得出结果：

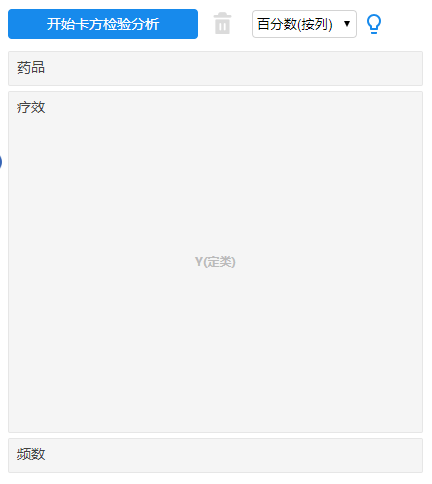
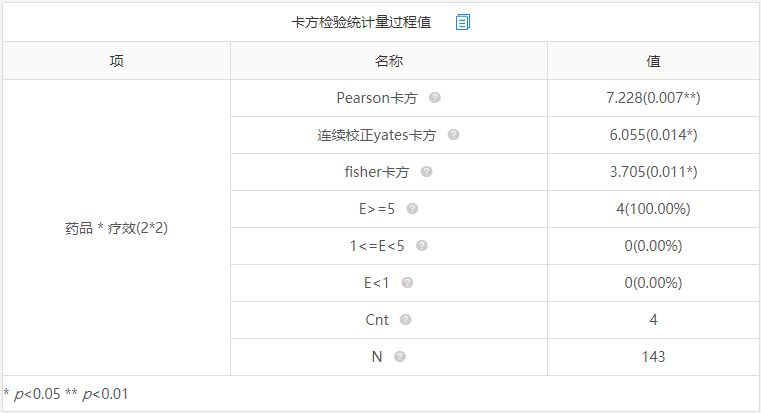
• 卡方检验增加了一些过程值的输出，原因在于实验研究中样本个数通常比较少，而默认使用的pearson卡方，要求总样本量n≥40，且所有的期望频数E≥5。
• 当n≥40且存在任意一个1 ≤E<5，则使用yates校正卡方。
• 当n<40，或E<1时，则用Fisher卡方。

这一选择过程SPSSAU会自动进行判断，并输出适合的卡方值及结果，直接使用该结果即可。

深入指标反映的是变量之间的相关程度，即在分析结果已经得出P<0.05，两种药物治疗感冒的疗效确实存在显著性差异时，进一步比较两种药品的疗效差异幅度究竟有多大。

SPSSAU提供了五个指标，分别对应不同的情况。可结合给出的”分析建议”进行选择，帮助手册中也有对应说明。

更多内容登录SPSSAU官网查看：

SPSSAU：方差分析、T检验、卡方分析如何区分？

SPSSAU：全流程总结相关分析

SPSSAU：T检验分析思路完整总结

你好！欢迎参加《小白爱上SPSS》课程，更多内容敬请期待！

第十六讲：多组率卡方检验和和Fisher确切法

今天我们来学习一下多组率卡方检验和Fisher确切法。当你数据的分组变量是2个水平或者多个水平，结局变量为二分类或者多分类数据，那么就可以多组率的形式开展描述和统计分析。与上一节的两组率的分析策略类似，可采用卡方检验（Χ2检验，Chi-square）和Fisher确切概率法，但细节方面有些差异。

第一，多行多列交叉表分析没有校正卡方。具体应用条件如下：

【1】不超过20%单元格的理论频数（期望频数）T < 5时，可使用卡方检验进行比较。

不超过20%的T < 5，卡方检验

【2】如果超过20%单元格的理论频数（期望频数）T < 5，或者至少一个T<1，此时采用的是Fisher确切概率法。

超过20%的T < 5或至少1个T ＜1 ，Fisher确切概率法

第二，多个率、多个构成比的卡方检验存在多重比较的步骤

多个率、多个构成成比较，就如方差分析一样，当P<0.05时，只能说明总体上存在着统计学差异，还不能说任意两组都有差异，需要多重比较进行进一步分析。

小白想知道橡胶、公路、跑步机、混合4种运动场地与运动损伤(是、否)之间的关系，应采用哪种统计分析方法？

（部分数据如下，完整数据请回复【小白数据】下载）

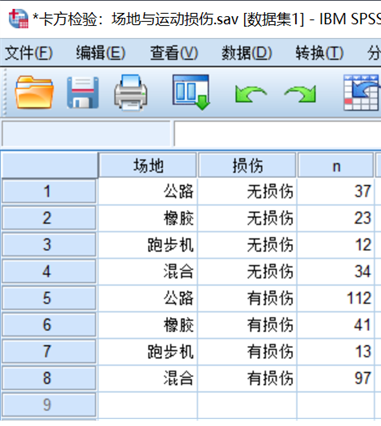
统计分析策略口诀“目的引导设计，变量确定方法”（啥意思？请点击此处复习一张脑图搞定！统计方法选择）

针对上述案例，扪心五问。

Q1：本案例研究目的是什么？

A：比较多组率差异。

比较四种运动场地与损伤（是、否）之间的差异。

Q2：比较的组数是多少呢？

A：四组数据。为4行2列类型数据。

Q3：本案例属于什么研究设计？

A：调查性研究，也可用于实验性研究。

Q4：有几个变量？

A：有两个变量。

自变量为四种运动场地

二分类结局变量为损伤（是、否）

Q5：变量类型是什么？

A：一个分组（分类）变量，分为橡胶、公路、跑步机、混合四种场地

另一个为二分类结局变量是有没损伤。

概括而言，如果数据满足以下条件，则采用多组率卡方检验或Fisher确切法

Step1: 先点击“数据——个案加权”。

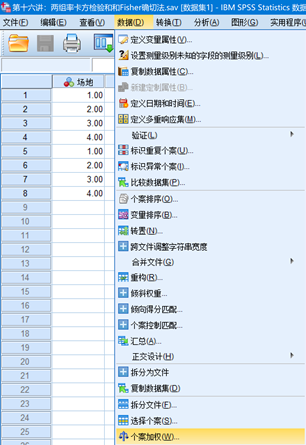
Step2：在弹出的对话框中，点击“个案加权系数”再把“频率变量f”放入对话框中，设置完后，点击“确定”后再关闭窗口。

Step1：依次点击“分析——描述统计 ——交叉表”。

Step2：在弹出“交叉表”对话框中，分别选择分组变量和结局变量到“行”和“列”中。

Step3：单击右侧的“精确”按钮，点击“精确”按钮。设置完后，点击“继续”。

Step4：单击右侧的“统计”按钮，勾选“卡方”。设置完后，点击“继续”。

Step5：单击右侧的“单元格”，勾选“实测”和勾选计算百分比中的“行”。设置完后，点击“继续”。

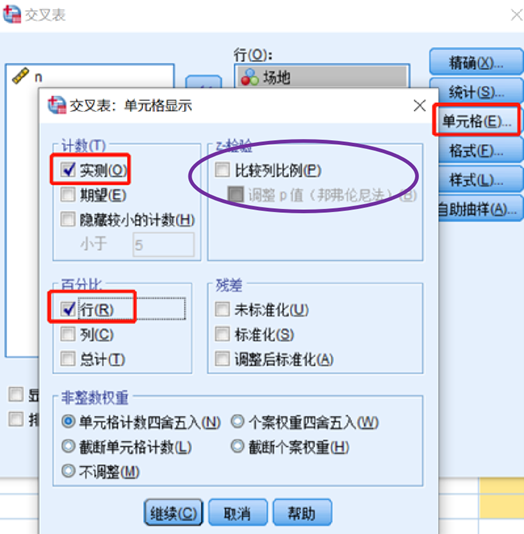
注意：在该对话框中有右边有“比较列比例”，此对话框的作用是当卡方达到显著性水平，可采用BONFERRONI进行校正，进行两两比较（类似单因素均数多重比较）。多重比较结果呈现在描述统计中，采用字母标注法。由于本研究不知卡方检验是否达到显著性水平，故暂时不选择。

Step6：完成上述参数设置后，在主对话框中单击“确定”按钮运行。

卡方检验的结果有多个表格，在此讲解两个重点表格。

第一，分组统计描述结果，分别有四种场地各自的损伤情况，包括发生数以及相应的百分比。

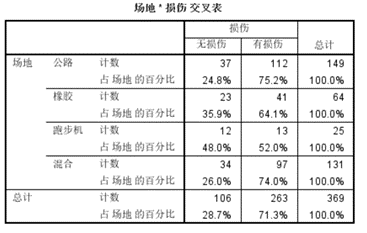
第二，卡方检验。要关注以下第二是表格下方注释a的理论（期望）频数，T最小值=7.18，所有T≥ 5，因此采用第一行“皮尔逊卡方”。

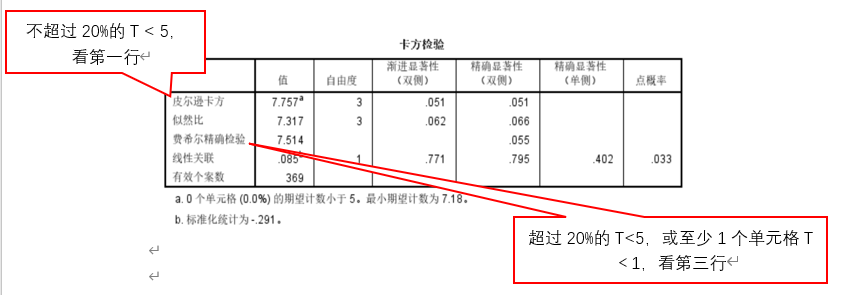
从表格中可知，Χ2=7.757, p=0.051, 未达到显著水平，故不进行多重比较。

规范报告有多种方式，本公众号只提供一种方式供参考。

表 四种运动场地与损伤（是、否）之间的卡方分析

卡方检验结果显示，4种运动场地的损伤率无显著性差异，Χ2=7.757，p=0.051.

小白学完了独立样本的卡方检验和Fisher确切法，赶紧查看了关于率的最后一讲，配对设计卡方检验。

1、当研究数据分成多组，结局变量为二分类或多分类数据，可采用卡方检验或Fisher确切概率法。

2、若不超过20%单元格的理论频数T < 5时，可采用卡方检验；若超过20%单元格的理论频数T < 5，或者至少一个T<1，则采用Fisher确切概率法。

3、当卡方检验结果有显著性差异，即P<0.05时，则还需进一步多重比较，在SPSS软件中可选择采用Bonferroni进行校正。

卡方检验，是常用的数据分析方法之一。然而，很多数据分析入门级选手没有数统专业的背景，对于卡方检验上手较慢。正所谓“基础不牢，地动山摇。”没有扎实的知识储备，很难迅速提升数据分析能力。

今天，我就一文整理全知乎最干货的【卡方检验】精华帖，让你搞懂基础知识的同时，也一步一步教会你做卡方检验。

通常理解的卡方检验，其检验目的在于定类和定类数据的差异。比如性别和是否戴眼镜的关系，性别和是否戴眼镜都是定类数据，因此可以研究性别和是否戴眼镜的比例是否有明显的差异性。

在实际使用过程中，卡方检验还可用于问卷多选题的分析（也称作多重响应分析），比如多选题的选择比例是否均匀，也或者单选题和多选题之间的差异关系情况如何呢，均可使用卡方检验进行分析。下表格为卡方检验的实际使用类型说明：

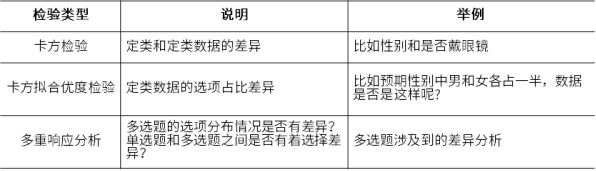
点击下方链接可以查看几类卡方检验的对比和说明：

使用卡方检验时，数据格式非常重要，因为SPSSAU支持加权和非加权两种格式，而且有时想利用卡方检验查看相关关系情况，此时还需要看一些新的指标，比如列联系数、Cramer V或Lambda指标等。当然还会有一些其它问题，汇总如下图：

完整版卡方检验实用总结：

了解了何为卡方检验，接下来我们看看如何通过卡方检验得到分析结果。

下面这篇文章提供了两种工具的操作步骤：

作为SPSSAU的野生代言人，我必须在此推荐这个“一分钟出结果”的高效数据分析网站，分析方法非常齐全，做卡方检验更是快上加快。

感兴趣的朋友可以点击下方链接了解~

完整版操作文章，请点击下方文章查看：

卡方检验是差异研究分析方法中的一种。差异研究的目的在于比较两组数据或多组数据之间的差异，通常包括以下几类分析方法，分别是方差分析、T检验和卡方检验。

三者简单区分如下图所示：

其实核心的区别在于：数据类型不一样。如果是定类和定类，此时应该使用卡方分析；如果是定类和定量，此时应该使用方差或者T检验。

方差和T检验的区别在于，对于T检验的X来讲，其只能为2个类别比如男和女。如果X为3个类别比如本科以下，本科，本科以上；此时只能使用方差分析。

进一步细化的区别，可以点击下文查看：

如果你觉得上面的文章还是很抽象，那么，下面这四篇文章中的具体案例，会让你更加理解卡方检验：

在明晰卡方检验的三种分类的基础上，入门级选手不仅要学会做卡方检验，更要学会选择合适的卡方检验类型完成数据分析。下面这篇文章列举了在不同场景下卡方检验的应用总结。

Pearson卡方可用研究定类和定类数据的差异，比如性别和是否吸烟之间的差异关系。

SPSSAU通用方法里面的‘交叉（卡方）’研究方法默认使用Pearson卡方，并且提供百分比按行或者按列两种方式。如下图：

完整版文章请点击下方链接查看：

卡方检验研究X和Y的差异，X和Y均是类别数据。当前需要进一步考虑另一个干扰因素分层项。比如是否吸烟（X)与是否生病(Y)的关系时，将性别纳入考虑范畴（即混杂因素,分层项Factor）。此时则称为分层卡方，分层卡方也称为Cochran-Mantel-Haenszel检验（CMH检验），分层卡方可以很好的解决‘辛普森悖论’问题。SPSSAU支持2*2*K结构数据（即X和Y均为2分类，K层）。

针对分层卡方，其涉及以下理论知识内容，如下表格：

通常情况下，首先查看‘比值比齐性检验’，如果其呈现出显著性（p 值小于0.05），则说明具有混杂因素，即需要考虑分层项，即分别查看不同分层项下的数据结果。反之如果没有通过‘比值比齐性检验’，即说明没有混杂因素不需要考虑分层项，报告整体的结果即可（包括卡方检验，以及OR值）。 Cochran–Mantel–Haenszel条件独立性用于研究考虑混杂因素（分层项）后，X与Y之间是否还存在着差异关系，相对意义较小。

同样的，分层卡方也可以使用SPSSAU分析，具体操作步骤点击下方链接查看：

问卷中如果有多选题，很可能会涉及多选题与其他题目的交叉分析。

具体如何进行分析呢，点击下方链接查看：

以上就是今天分享的全部内容啦~

更多干货集合贴推荐：

Chi-squared检验是假设检验的一种，可以用来检验关于分类变量的说法。如果你想了解卡方检验、T检验和方差分析之间的区别，请阅读这篇文章

让我们先了解一下卡方检验可以用样本解决什么样的问题。我们有一个电影类型的列表，这是第一个变量；第二个变量是这些电影类型的观众是否在电影院里买零食。我们的想法（或者用统计学术语来说，我们的原假设）是，电影类型与观众是否购买零食无关。电影院老板想估计他们需要购买多少零食。在这个例子中，电影类型和是否买零食都是分类变量，所以卡方检验可以发挥作用。
下面是另一个例子。假设我们推出一个新产品，我们想知道我们是否应该为男性和女性做不同的宣传。但在这之前，我们需要回答性别是否会影响销售。这里的性别和购买与否都是分类的。
第三个例子。假设有一个服装品牌，生产不同尺寸和颜色的衬衫。现在从库存的角度来看，很难向所有的零售商提供所有颜色和尺寸的组合。因此，我们决定评估消费者的尺寸和颜色偏好之间是否存在某种关系。这里颜色和尺寸都是分类变量。

在了解了Chi-squared检验的工作情况后，让我们来探讨一下该检验的工作原理。

下面是一个案例。一家药物测试实验室随机选择了574名成年人来研究抗生素的耐药性（如下图所示）。问：这两个人群的耐药率是否一致？

原假设：两个人群之间的耐药率是一致的。

在一个数据样本中，属于某个特定组别的数据数量被称为频数，所以分类数据的分析就是频数分析。 在我们的案例中，包括180、215、73和106等数字都是频数。

当n是上表中观察值的总数时，表中每个单元格的期望值为

让我们通过上述公式计算预期值：

现在，我们有实际频数和预期频数，为了帮助你理解，我把它们写成一对：（180,174.10），（215,220.90），（73,78.90），（106,100.1）。

检验统计量的计算为： ， 是每观察值，也就是实际频数，而 是与之相对应的期望频数。

在我们的例子中，统计值为

接下来，我们需要根据自由度和显著性水平查询chi-square表以获得临界值。由于频率表是2x2（2行2列，我们只关心频率），所以自由度是（2-1）*（2-1）=1。我们选择0.05作为显著性水平，得到的临界值为3.841，大于统计值1.146，所以我们不能拒绝原假设。

另外，Scipy可以简化计算工作。下面是代码

from scipy import stats
  
observed = [73,106,215,180]
expected = [78.9,100.1,220.9,174.1]
stats.chisquare(f_obs = observed,
                f_exp = expected)

# Power_divergenceResult(statistic=1.1464688075625198, pvalue=0.7658697980039403)
# We can see the result is the same as we calculated by hand.

摘要：在这篇文章中，我介绍了什么是卡方检验以及如何手动和使用Scipy计算统计值。