数学 ｜ 小学数学必会图形求面积的10个方法！图文并茂，太神奇了！

小学数学学过的几何图形有三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形，这些几何图形一般称为基本图形或规则图形，我们的面积及周长都有相应的公式直接计算。如下表：

实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算。一般我们称这样的图形为不规则图形。那么，不规则图形的面积及周长怎样去计算呢？

我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

例1：如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米求阴影部分的面积。

一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等，都等于正方形ABCD面积的三分之一，也就是12厘米.

解：

S△ABE=S△ADF=S四边形AECF=12

在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，

∴△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3：两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。如右图那样重合.求重合部分（阴影部分）的面积。

常用的基本方法

1 相加法

这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。

例如：求下图整个图形的面积。

3 直接求法

这种方法是根据已知条件，从整体出发直接求出不规则图形面积。

例如：下图，求阴影部分的面积。

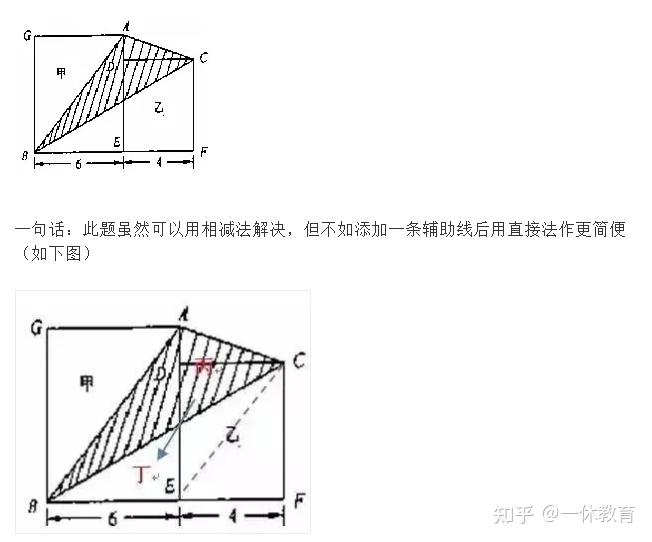
根据梯形两侧三角形面积相等原理（蝴蝶定理），可用三角形丁的面积替换丙的面积，组成一个大三角ABE，这样整个阴影部分面积恰是大正方形面积的一半。

6 割补法

这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决。

例如：下图，若求阴影部分的面积。

一句话：可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

8 旋转法

这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积。

例如：下图（1），求阴影部分的面积。

9 对称添补法

这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半。

例如：下图，求阴影部分的面积。

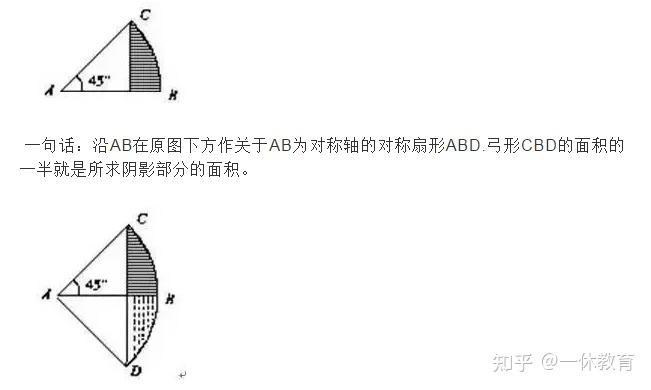
10 重叠法

这种方法是将所求的图形看成是两个或两个以上图形的重叠部分。

例如：下图，求阴影部分的面积。